MODULE FOR DIFFUSION PROBLEMS More...
Data Types | |
| interface | l2_product |
| L2 product of a function with the basis functions. More... | |
Functions/Subroutines | |
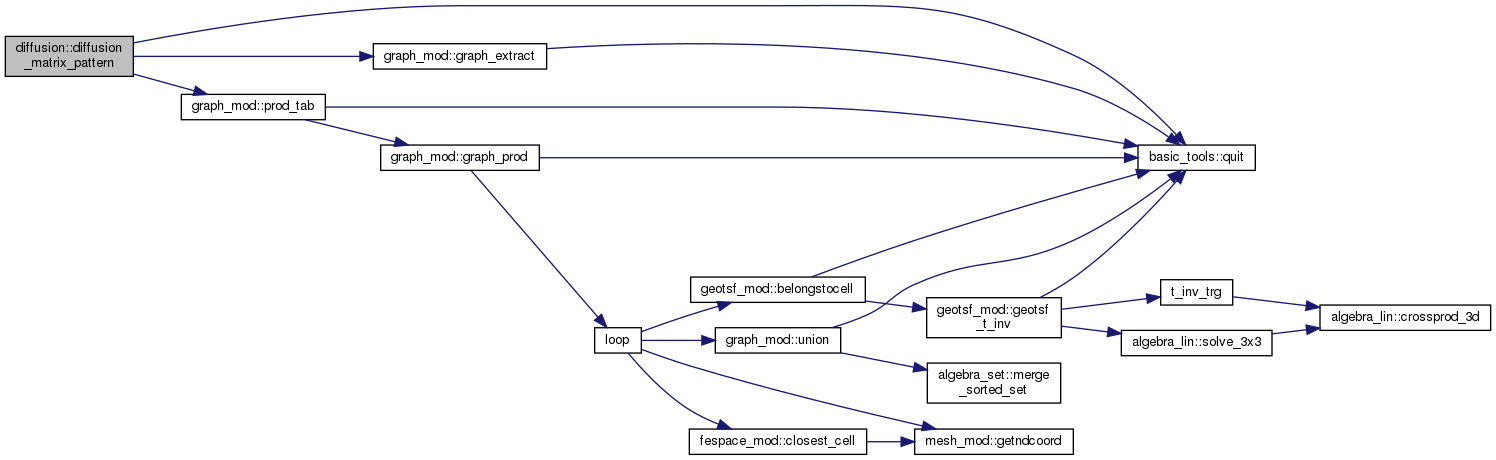
| subroutine, public | diffusion_matrix_pattern (g, X_h, qdm) |
| Define the sparsity pattern for diffusion matrices More... | |
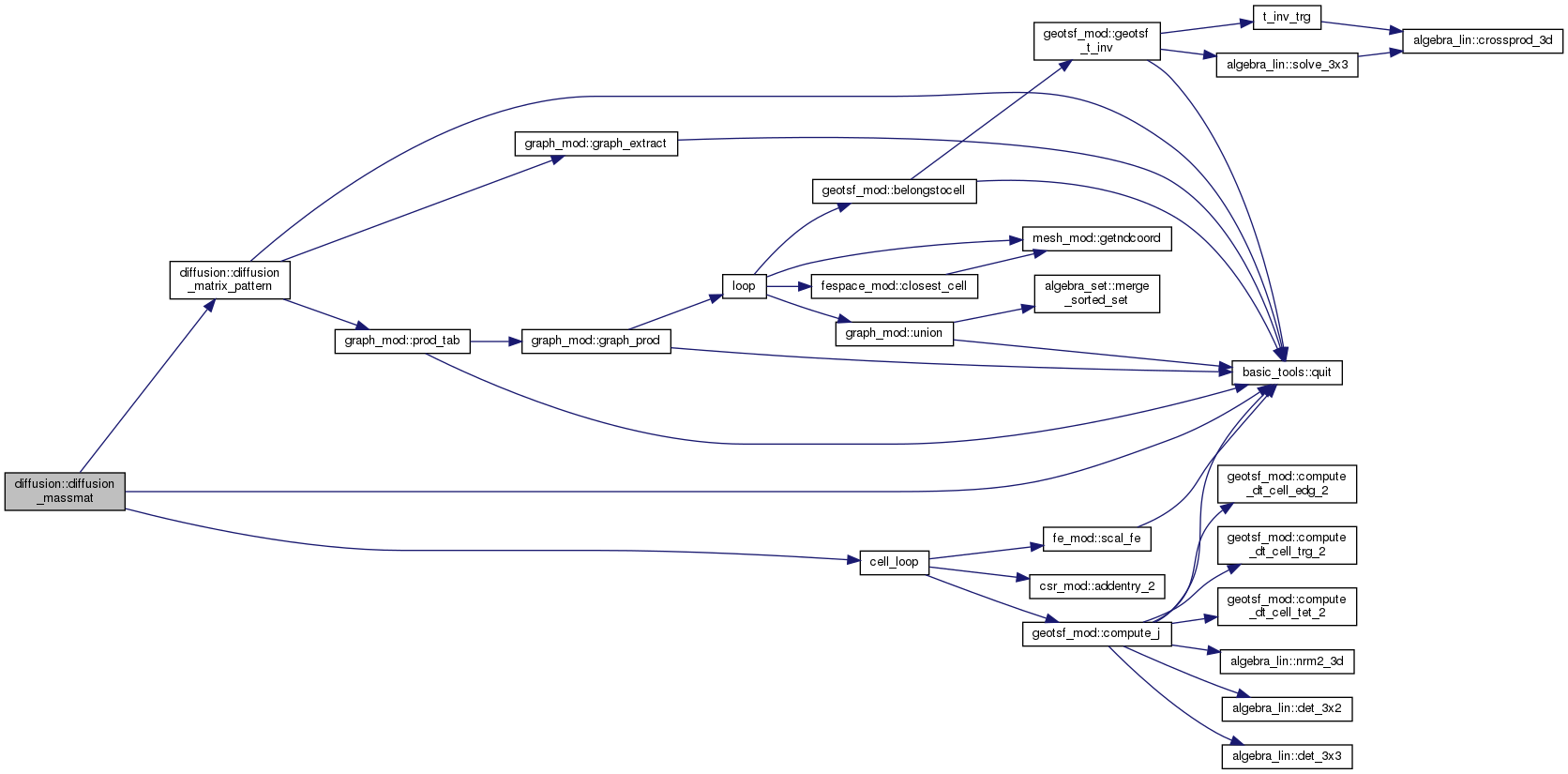
| subroutine, public | diffusion_massmat (mass, a, X_h, qdm, dofToDof) |
| Assemble the mass matrix of the bilinear product: More... | |
| subroutine, public | diffusion_stiffmat (stiff, b, X_h, qdm, dofToDof) |
| Assemble the stiffness matrix of the bilinear product: More... | |
| subroutine, public | diffusion_neumann_rhs (rhs, g, X_h, quad_type, f) |
| L2 scalar product of a scalar function \( g \) with the basis functions fo the finite element space \( X_h \) on \(\Gamma_f \subset \partial\Omega\) a part of the domain boundary. More... | |
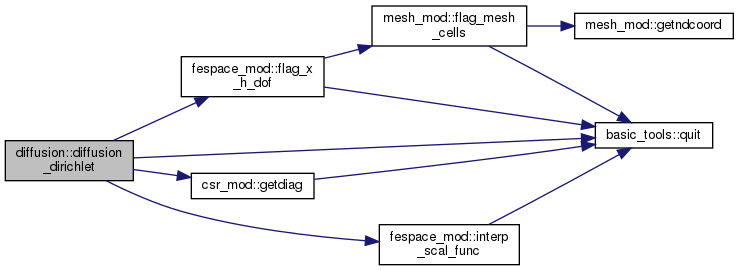
| subroutine, public | diffusion_dirichlet (K, rhs, g, X_h, rho, f) |
| DIRICHLET BOUNDARY CONDITION FOR A DIFFUSION PROBLEM More... | |
| subroutine | fespace_l2_product (FV, f, X_h, qdm) |
| L2 Product of a scalar function \( f:~\R^3 \mapsto \R\) with the basis functions of a scalar finite element space. More... | |
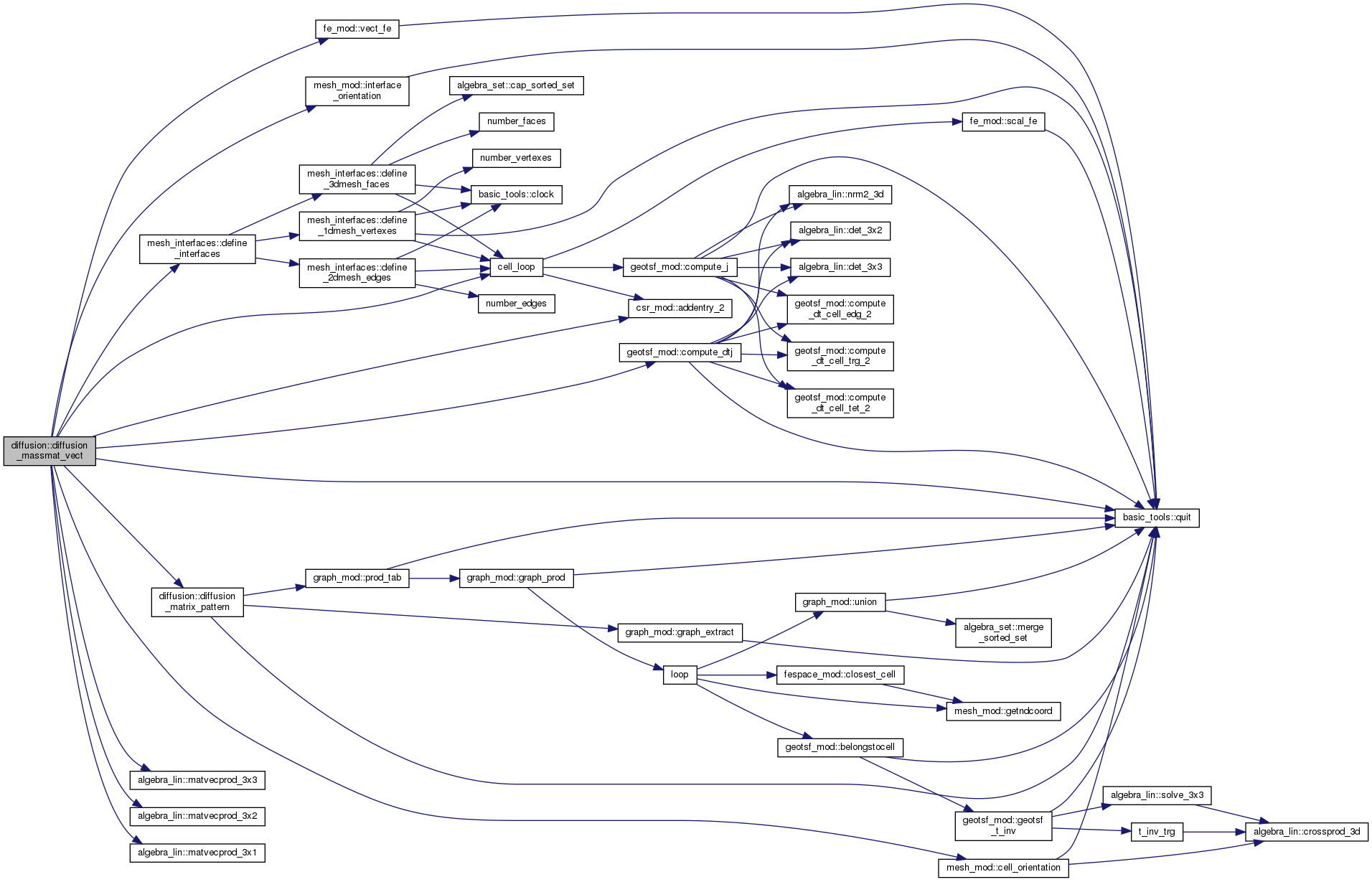
| subroutine, public | diffusion_massmat_vect (mass, b, X_h, qdm, dofToDof) |
| Assemble the mass matrix of the bilinear product: More... | |
| subroutine, public | diffusion_mixed_divmat (divMat, X_s, X_v, qdm) |
| Assemble the matrix of the bilinear product: More... | |
Detailed Description
MODULE FOR DIFFUSION PROBLEMS
A module for diffusion equations of the form
\(~~~~~~~~~~~~~~~~~~\) \(~~~~~~~~~ -\dv(B(x) \nabla u) + \rho(x) u = f \)
with \( B(x)\) a diffusivity tensor.
Tutorial examples:
- poisson_2d.f90: Poisson problem in 2D.
- diffusion_Neumann.f90: a general diffusion equation with Neumann boundary condition.
- diffusion_Dirichlet_Neumann.f90: a general diffusion equation with mixed Dirichlet-Neumann boundary condition.
Function/Subroutine Documentation
◆ diffusion_dirichlet()
| subroutine, public diffusion::diffusion_dirichlet | ( | type(csr), intent(inout) | K, |
| real(rp), dimension(:), intent(inout) | rhs, | ||
| procedure(r3tor) | g, | ||
| type(fespace), intent(in) | X_h, | ||
| real(rp), intent(in) | rho, | ||
| procedure(r3tor), optional | f | ||
| ) |
DIRICHLET BOUNDARY CONDITION FOR A DIFFUSION PROBLEM
Given:
- the boundary sub-domain
\[ \Gamma_f = \partial\Omega \cap \{f\ge 0\}, \]
- the source term \( g \) on \( \Gamma_f \).
- the linear ssytem
\[ K U = \text{rhs}, \]
- the penalty coefficient \( \rho \gg 1 \),
Penalise the linear system on the lines i associated with a finite element node \( x\in \Gamma_f \):
- rhs(i) = rhs(i) + \( \rho g(x)\)
- \( K_{i,i} = K_{i,i} + \rho \)
INPUT:
- \( K\), rhs the original matrix and right hand side of the system,
- \( g:~\R^3 \mapsto \R \)
- \( X_h \) a scalar finite element space on a mesh of the domain \( \Omega \)
- rho = penalty coefficient$
- \( f:~\R^3 \mapsto \R \) a function to characterise the boundary sub-domain \(\Gamma_f = \partial\Omega \cap \{f\ge 0\} \).
This is an optional argument, if not provided \( \Gamma_f = \partial\Omega \).
OUTPUT:
- \( K\), rhs the penalised matrix and right hand side of the system,
Definition at line 656 of file diffusion.F90.
◆ diffusion_massmat()
| subroutine, public diffusion::diffusion_massmat | ( | type(csr), intent(inout) | mass, |
| procedure(r3tor) | a, | ||
| type(fespace), intent(in) | X_h, | ||
| type(quadmesh), intent(in) | qdm, | ||
| type(graph), intent(in), optional | dofToDof | ||
| ) |
Assemble the mass matrix of the bilinear product:
\( (u,v) \mapsto \int_O a(x)~ u(x) v(x) \dx ~~\in\R\)
- \( u, v \in X_h = \) scalar finite element space on the mesh \( \T \).
- \( O \) = integration domain, see quadmesh_mod for a definition.
OUTPUT:
- mass= mass matrix
INPUT :
- \( a:~x \in\R^3 \mapsto a(x)\in\R \), density function
- \( X_h =\) scalar finite element space on the mesh \( \T \)
- qdm = integration method on the mesh \( \T \)
- dofToDof = connectivity graph DOF –> DOF (optional, of type graph_mod::graph)
Definition at line 168 of file diffusion.F90.
◆ diffusion_massmat_vect()
| subroutine, public diffusion::diffusion_massmat_vect | ( | type(csr), intent(inout) | mass, |
| procedure(r3xr3xr3tor) | b, | ||
| type(fespace), intent(in) | X_h, | ||
| type(quadmesh), intent(in) | qdm, | ||
| type(graph), intent(in), optional | dofToDof | ||
| ) |
Assemble the mass matrix of the bilinear product:
\( (p,q) \mapsto \int_O b(x, p(x), q(x)) \dx ~~\in\R\)
- \( p, q \in X_h = \) vector finite element space on the mesh \( \T \).
- \( O \) = integration domain, see quadmesh_mod for a definition.
OUTPUT:
- mass= mass matrix
INPUT :
- \( b:~ (x, \xi_1, \xi_2) \in \R^3 \times \R^3 \times \R^3 \mapsto b(x, \xi_1, \xi_2) \in \R \)
assumed to be bilinear and symmetric in \(\xi_1\) and \( \xi_2\).
This assumption must be respected, it is not checked.
- \( X_h =\) vector finite element space on the mesh \( \T \) (of type fespacexk_mod::fespacexk)
- qdm = integration method on the mesh \( \T \) (of type quadmesh_mod::quadmesh)
- dofToDof = connectivity graph DOF –> DOF (optional, of type graph_mod::graph)
Definition at line 899 of file diffusion.F90.
◆ diffusion_matrix_pattern()
| subroutine, public diffusion::diffusion_matrix_pattern | ( | type(graph), intent(inout) | g, |
| type(fespace), intent(in) | X_h, | ||
| type(quadmesh), intent(in) | qdm | ||
| ) |
Define the sparsity pattern for diffusion matrices
It is given by the connectivity graph Dof –> Dof:
between the degrees of freedom of the finite element space \( X_h \) on the mesh \( \T \).
DOF_i is in relation with DOF_j if:
- they are asociated to a common cell of the mesh \( \T \),
- and if that common cell is associated to a non-void quadrature rule in the integration method.
OUTPUT:
- g = connevtivity graph
INPUT :
- \( X_h \) finite element space on the mesh \( \T \)
- qdm = integration method on the mesh \( \T \)
Definition at line 96 of file diffusion.F90.
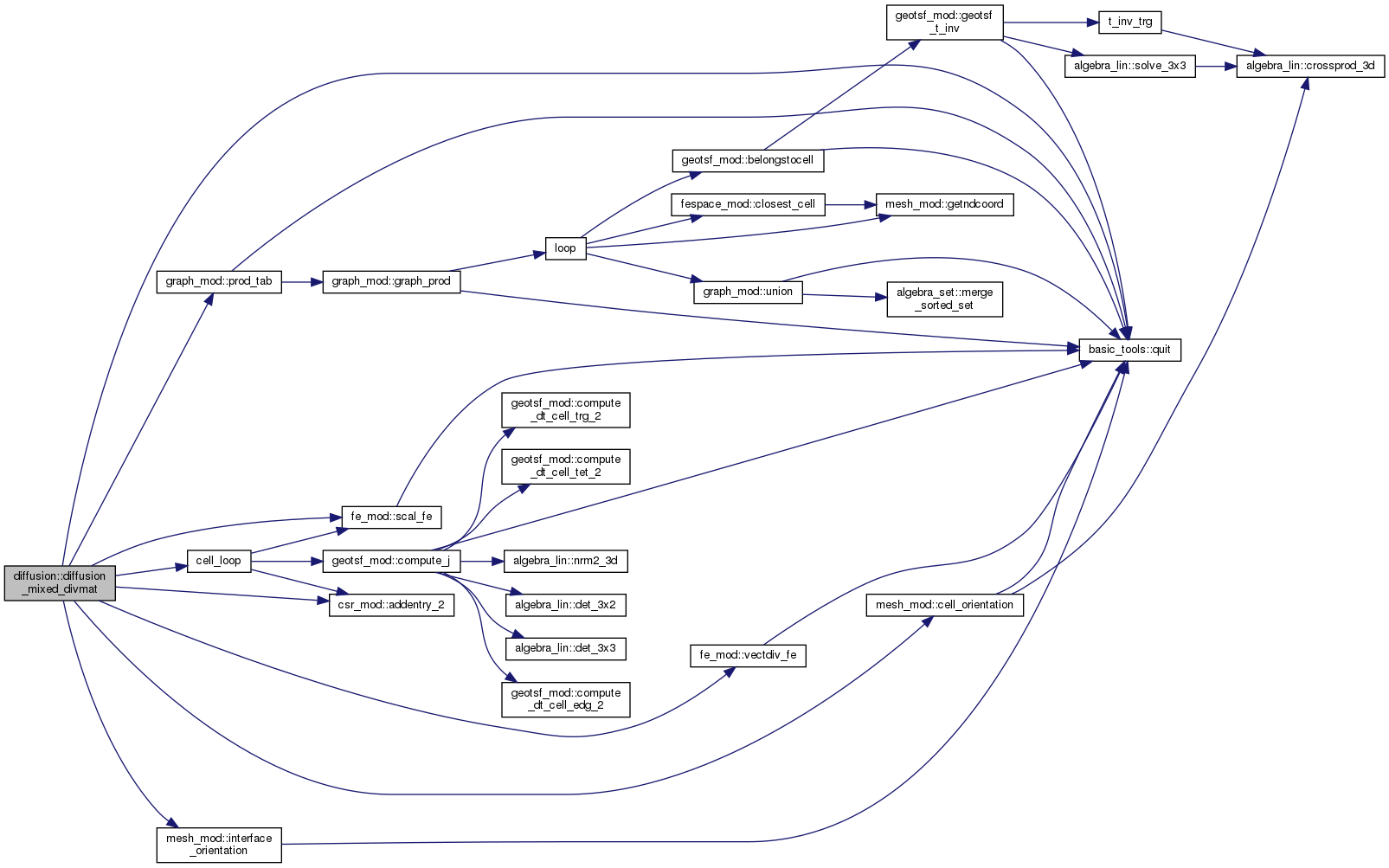
◆ diffusion_mixed_divmat()
| subroutine, public diffusion::diffusion_mixed_divmat | ( | type(csr), intent(inout) | divMat, |
| type(fespace), intent(in) | X_s, | ||
| type(fespace), intent(in) | X_v, | ||
| type(quadmesh), intent(in) | qdm | ||
| ) |
Assemble the matrix of the bilinear product:
\( (u,p) \mapsto \int_O u(x) \dv p(x) \dx ~~\in\R\)
- \( u \in X_s = \) scalar finite element space on the mesh \( \T \).
- \( p \in X_v = \) vector finite element space on the mesh \( \T \).
- \( O \) = integration domain, see quadmesh_mod for a definition.
OUTPUT:
- divMat= matrix of the product
INPUT :
- \( X_s =\) scalar finite element space on the mesh \( \T \)
- \( X_v =\) vector finite element space on the mesh \( \T \)
- qdm = integration method on the mesh \( \T \)
Definition at line 1164 of file diffusion.F90.
◆ diffusion_neumann_rhs()
| subroutine, public diffusion::diffusion_neumann_rhs | ( | real(rp), dimension(:), allocatable | rhs, |
| procedure(r3tor) | g, | ||
| type(fespace), intent(in) | X_h, | ||
| integer, intent(in) | quad_type, | ||
| procedure(r3tor), optional | f | ||
| ) |
L2 scalar product of a scalar function \( g \) with the basis functions fo the finite element space \( X_h \) on \(\Gamma_f \subset \partial\Omega\) a part of the domain boundary.
INPUT:
- \( g:~\R^3 \mapsto \R \)
- \( X_h \) a scalar finite element space on a mesh of the domain \( \Omega \)
- 'quad_type' quadrature rule for the boundary cells \( K \subset \Gamma_f\)
- \( f:~\R^3 \mapsto \R \) a function to characterise the boundary sub-domain \(\Gamma_f = \partial\Omega \cap \{f\ge 0\} \).
This is an optional argument, if not provided \( \Gamma_f = \partial\Omega \).
OUTPUT:
- rhs = \( (g_i)_{1\le i\le N} \) with \( g_i = \int_{\Gamma_f} g(x) v_i \dx \), where \( (v_i)_{1\le i\le N} \) are the basis functions of \( X_h\).
Definition at line 590 of file diffusion.F90.

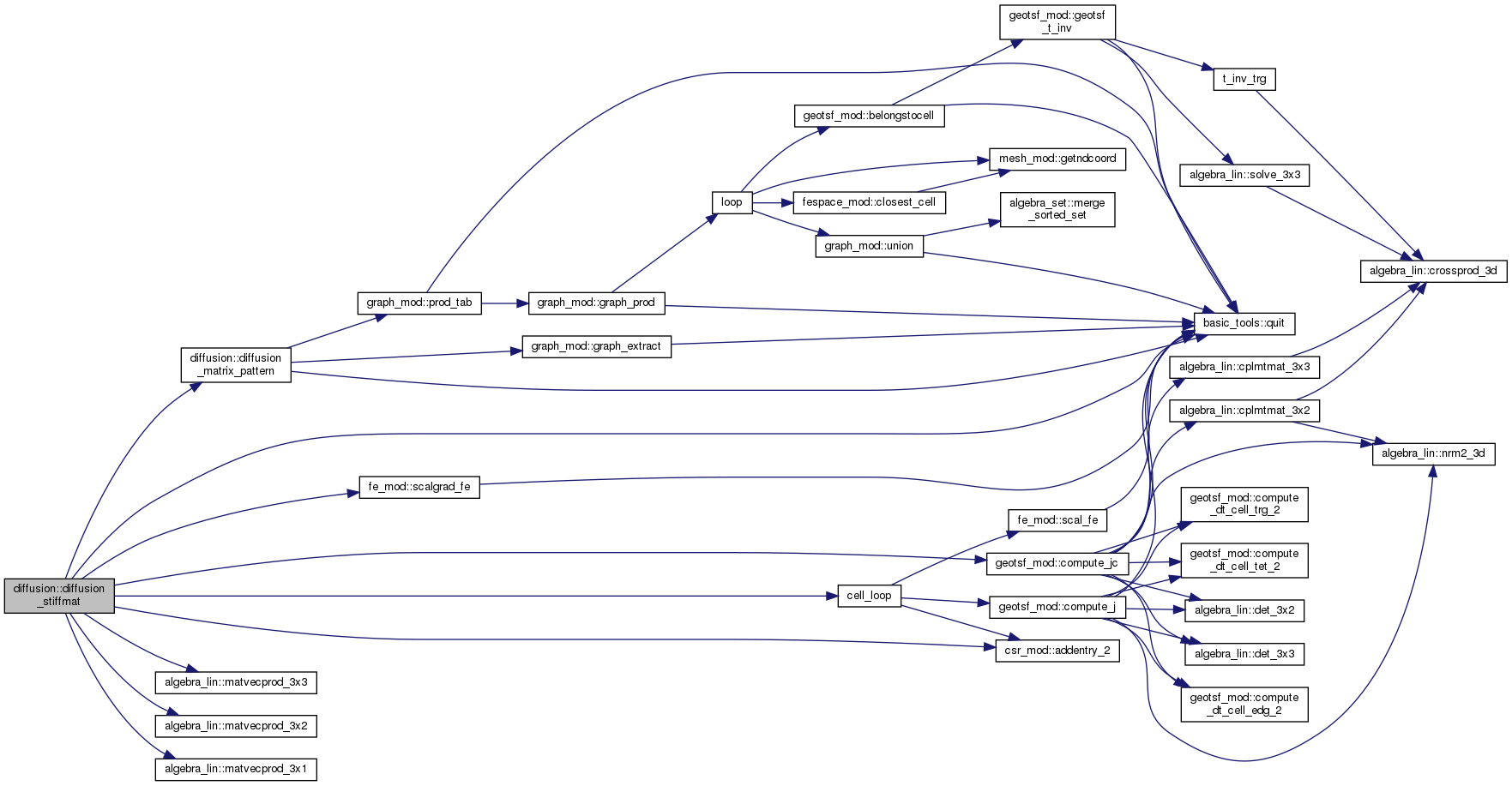
◆ diffusion_stiffmat()
| subroutine, public diffusion::diffusion_stiffmat | ( | type(csr), intent(inout) | stiff, |
| procedure(r3xr3xr3tor) | b, | ||
| type(fespace), intent(in) | X_h, | ||
| type(quadmesh), intent(in) | qdm, | ||
| type(graph), intent(in), optional | dofToDof | ||
| ) |
Assemble the stiffness matrix of the bilinear product:
\( (u,v) \mapsto \int_O b(x, \nabla u(x), \nabla v(x)) \dx ~~\in\R\)
- \( u, v \in X_h = \) scalar finite element space on the mesh \( \T \).
- \( O \) = integration domain, see quadmesh_mod for a definition.
OUTPUT:
- stiff= stiffness matrix
INPUT :
- \( b:~ (x, \xi_1, \xi_2) \in \R^3 \times \R^3 \times \R^3 \mapsto b(x, \xi_1, \xi_2) \in \R \)
assumed to be bilinear and symmetric in \(\xi_1\) and \( \xi_2\).
This assumption must be respected, it is not checked.
- \( X_h =\) scalar finite element space on the mesh \( \T \) (of type fespacexk_mod::fespacexk)
- qdm = integration method on the mesh \( \T \) (of type quadmesh_mod::quadmesh)
- dofToDof = connectivity graph DOF –> DOF (optional, of type graph_mod::graph)
NOTE : every cell \(K \subset O\) is either
- an open domain in \(\R^3\)
- a parametrised surface in \(\R^3\)
- a parametrised curve in \(\R^3\)
In the 2nd and 3rd cases : \( \nabla u(x)\) is in the tangent gradient (in the tangent space).
Definition at line 366 of file diffusion.F90.
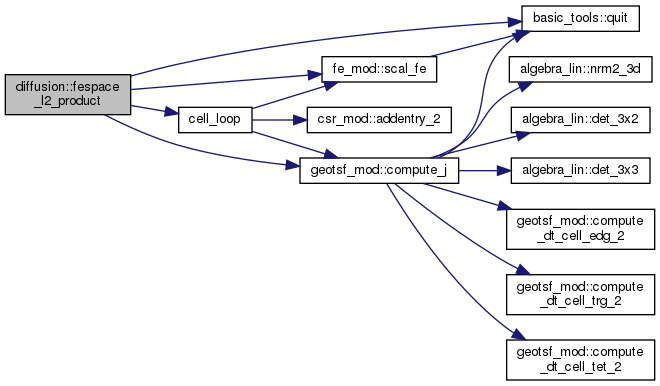
◆ fespace_l2_product()
|
private |
L2 Product of a scalar function \( f:~\R^3 \mapsto \R\) with the basis functions of a scalar finite element space.
INPUT
- \( f:~ \R^3 \mapsto \R\)
- \( X_h =\) scalar finite element space on the mesh \( \T \)
- qdm = integration method on the mesh \( \T \)
OUTPUT:
- \( FV = (FV_i)_{1\le i\le N} \) with \( FV_i = \int_O f(x) v_i(x) \dx = [ (f,u_i)_{{\rm L}^2(O)} ] \)
where the \( (v_i)_{1\le i\le N} \) are the basis function of \( X_h \).
- \( O \) = integration domain, see quadmesh_mod for a definition.
Definition at line 741 of file diffusion.F90.
 1.8.13
1.8.13