Functions/Subroutines
program	diffusion_dirichlet_neumann
	SOLVES THE DIFFUSION PROBLEM with mixed Dirichlet / Neumann boundary conditions More...

real(rp) function	u (x)
	exact solution 'u' More...

real(rp) function, dimension(3)	grad_u (x)
	gradient of the exact solution More...

real(rp) function	f (x)
	right hand side 'f' More...

real(rp) function	x_le_0 (x)
	To characterise {x=0}. More...

real(rp) function	x_ge_1 (x)
	To characterise {x=1}. More...

real(rp) function	y_le_0 (x)
	To characterise {x=0}. More...

real(rp) function	y_ge_1 (x)
	To characterise {x=1}. More...

real(rp) function	dx_u_1 (x)
	u on {x=1} More...

real(rp) function	dy_u_1 (x)
	u on {y=1} More...

Function/Subroutine Documentation

◆ diffusion_dirichlet_neumann()

program diffusion_dirichlet_neumann ( )

SOLVES THE DIFFUSION PROBLEM with mixed Dirichlet / Neumann boundary conditions

\(~~~~~~~~~ -\Delta u + u = f ~~~\) on \(~~~ \Omega= [0,1]^2 \)

Dirichlet boundary condition: \( u = g_D \) on \( \Gamma_D\subset \Gamma = \partial \Omega\):

\( u = 1+y^2 \) on \(\Gamma \cap \{x=0\} \)
\( u = \cos x \) on \(\Gamma \cap \{y=0\} \)

Neumann boundary condition: \( \nabla u\cdot n = g_N \) on \( \Gamma_N\subset \Gamma\):

\( \partial_x u = -\sin(1) (1+y^2) \) on \(\Gamma \cap \{x=1\} \)
\( \partial_y u = 2 \cos(x) \) on \(\Gamma \cap \{y=0\} \)

Volumic source term and exact solution:

\( u = cos(x) (1+y^2)\)
\( f = 2u -2 cos x\)

VARIATIONAL FORMULATION

The finite element space is \( X_h\subset \Hu\).

Let \( X_{h,D} \subset X_h\) the subspace of all functions vanishing on \( \Gamma_D \).

Numerical probelm: find \(u\in X_h\) such that \( ~~~~\forall ~v \in X_{h,D}, ~~~~ \)

\[ \int_\Omega \nabla u\cdot\nabla v \,\dx ~+~ \int_\Omega u\, v \,\dx ~=~ \int_\Omega f \, v \,\dx ~+~ \int_{\Gamma_N} g_N \, v \,\dx \]

and such that \( u(x_i) = g_D(x_i) \) for all finite element nodes \( x_i\in \Gamma_D\)

NUMERICAL RESOLUTION

The basis functions are \( (v_i)_{1\le i\le N} \) (basis of \(X_h\)).

By construction, a subset of the basis functions form a basis of \( X_{h,D}\).

Computation of the stiffness matrix
\[ S =[s_{i,\,j}]_{1\le i,\,j\le N}, \quad \quad s_{i,\,j} = \int_\Omega \nabla v_i\cdot\nabla v_j \,\dx \]

Computation of the mass matrix
\[ M =[s_{i,\,j}]_{1\le i,\,j\le N}, \quad \quad m_{i,\,j} = \int_\Omega v_i\, v_j \,\dx \]

Computation of the right hand side for the volumoc source term \( f \)
\[ F = (f_i)_{1\le i\le N}, \quad \quad f_i = \int_\Omega f \, v_i \,\dx \]

Computation of the right hand side for the surfacic source term \( g_N \)
\[ G_N = (g_i)_{1\le i\le N}, \quad \quad g_i = \int_{\Gamma_N} g_N \, v_i \,\dx \]

\( K = M + S \) and \( \text{RHS} = F + G_N \)

Penalisation of the linear system \( K U =\)RHS:

let \( 1\le i \le N \) be so that the finite element node \( x_i \in\Gamma_D\),
\( \text{RHS}_i =\text{RHS}_i + \rho g_D(x_i)\)
\( K_{i,i} =K_{i,i} + \rho \)
\(\rho \gg 1\) a penalisation coefficient.

Resolution of the (symmetric positive definite) system

\[ K U_h = \text{RHS}\]

POST TREATMENT

Computation of the numerical error between the exact solution \(u\) and the numerical solution \(u_h\),
\[ \int_\Omega |u-u_h|^2 \dx~,\quad\quad \int_\Omega |\nabla u-\nabla u_h|^2 \dx \]
Graphical display of the numerical solution with gmsh

Charles PIERRE, November 2019

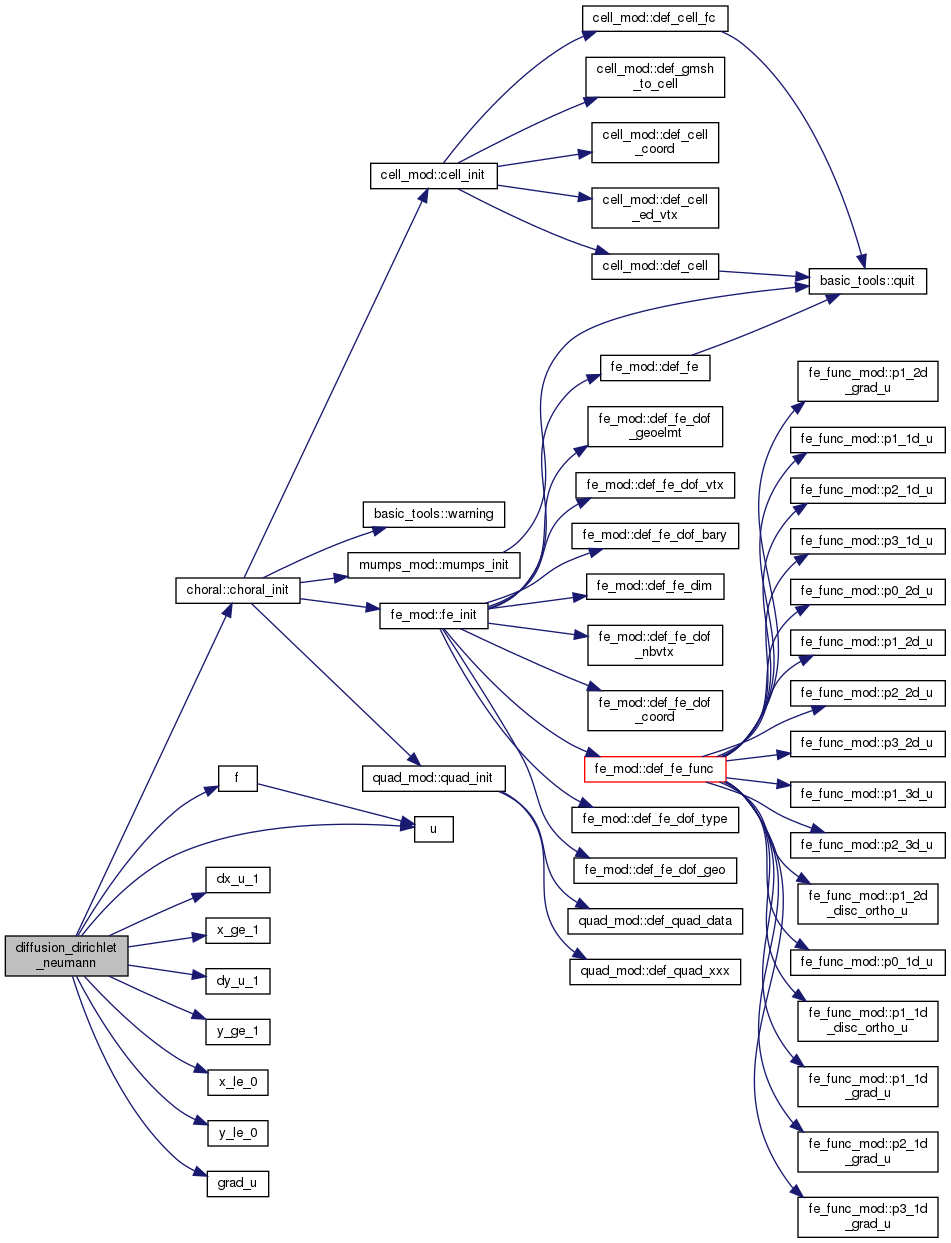
Definition at line 95 of file diffusion_Dirichlet_Neumann.f90.

Here is the call graph for this function:

◆ dx_u_1()

real(rp) function diffusion_dirichlet_neumann::dx_u_1 ( real(rp), dimension(3), intent(in) x )

u on {x=1}

Definition at line 397 of file diffusion_Dirichlet_Neumann.f90.

◆ dy_u_1()

real(rp) function diffusion_dirichlet_neumann::dy_u_1 ( real(rp), dimension(3), intent(in) x )

u on {y=1}

Definition at line 407 of file diffusion_Dirichlet_Neumann.f90.

◆ f()

real(rp) function diffusion_dirichlet_neumann::f ( real(rp), dimension(3), intent(in) x )

right hand side 'f'

Definition at line 342 of file diffusion_Dirichlet_Neumann.f90.

Here is the call graph for this function:

◆ grad_u()

real(rp) function, dimension(3) diffusion_dirichlet_neumann::grad_u ( real(rp), dimension(3), intent(in) x )

gradient of the exact solution

Definition at line 329 of file diffusion_Dirichlet_Neumann.f90.

◆ u()

real(rp) function diffusion_dirichlet_neumann::u ( real(rp), dimension(3), intent(in) x )

exact solution 'u'

Definition at line 318 of file diffusion_Dirichlet_Neumann.f90.

◆ x_ge_1()

real(rp) function diffusion_dirichlet_neumann::x_ge_1 ( real(rp), dimension(3), intent(in) x )

To characterise {x=1}.

Definition at line 365 of file diffusion_Dirichlet_Neumann.f90.

◆ x_le_0()

real(rp) function diffusion_dirichlet_neumann::x_le_0 ( real(rp), dimension(3), intent(in) x )

To characterise {x=0}.

Definition at line 354 of file diffusion_Dirichlet_Neumann.f90.

◆ y_ge_1()

real(rp) function diffusion_dirichlet_neumann::y_ge_1 ( real(rp), dimension(3), intent(in) x )