ionicmodel_mod Module Reference

DERIVED TYPE ionicModel: cellular ionic models in electrophysiology More...

Data Types
interface	clear
	destructor More...
interface	ionic_term
	Abstract interface: \( f:~ R \times R^n \mapsto R^n \times R^m \). More...
interface	ionicmodel
	DERIVED TYPE ionicModel: cellular ionic models in electrophysiology More...
interface	print
	print a short description More...

Functions/Subroutines
subroutine	ionicmodel_clear (im)
	Destructor. More...
type(ionicmodel) function	ionicmodel_create (type)
	Constructor for the type ionicModel More...
subroutine	ionicmodel_print (im)
	Print a short description. More...
subroutine, public	ionicmodel_ilist (I, Y, I_app, type)
	Membrane ionic currents More...

Detailed Description

DERIVED TYPE ionicModel: cellular ionic models in electrophysiology

Choral constants for ionic models in electrophysiology: IONIC_xxx, see the list.

An ionic model 'im' is created with

type(ionicmodel) :: im
...
im = ionicmodel(type)

with type any of IONIC_xxx

Mathematically, an ionic model is described with a variable \( Y\in\R^N\), \( Y = ^T[w,c,v]\):

• \( w \in \R^{N_w} \) a vector of gating variables
• \( c \in \R^{N-N_w-1} \) a vector of ionic concentrations,
• \( V \in \R \) the transmembrane potential.

The membrane equation is ruled by the ODE system
\(~~~~~ {\displaystyle \frac{dw_i}{dt} = \frac{w_i-w_{i,\infty}(Y, I_{\rm app})}{\tau_i(Y, I_{\rm app})} }\) \(~~~~~~~i=1\dots N_w\)
\(~~~~~ {\displaystyle \frac{dc_i}{dt} = g_i(Y, I_{\rm app}) }\) \(~~~~~~~~~~~~~~~~~~~~~~~i=1\dots N-N_w-1\)
\(~~~~~ {\displaystyle \frac{dV}{dt} = -\sum_{i=1}^{N_I} I_j(Y, I_{\rm app}) + I_{\rm app} }\)
with \( N_I\) the number of modelled membrane ionic currents, \( I_j(Y)\) each individual membrane ionic current and \( I_{\rm app}\) an external applied stimulation current.

The source term \(I_{\rm app} = I_{\rm app}(x,t)\) is not given by the model, it has to be defined by the user.

This formulation is general. It oftently has the simpler form:
\(~~~~ w_{i,\infty} = w_{i,\infty}(V), \quad \tau_{i} = \tau_i(V), \quad g_i = g_i(Y), \quad I_j = I_j(Y) \).

This is gathered in the ODE system \({\displaystyle \frac{dY}{dt} = F(Y,I_{\rm app}(t))}\) with \( F:~(Y,I)\in\R^N\times \R \rightarrow F(Y, I) \in\R^N \),

• \(~~~ {\displaystyle F_i(Y,I)= \frac{w_i-w_{i,\infty}(Y, I)}{\tau_i(Y, I)}}\) \(~~~~~~~~~~~~~~i=1\dots N_w\)
• \(~~~ {\displaystyle F_{i+N_w}(Y,I)= g_i(Y, I)}\) \(~~~~~~~~~~~~~~~~~~~~~~~i=1\dots N-N_w-1\)
• \(~~~ {\displaystyle F_N(Y,I) = -\sum_{i=1}^{N_I} I_j(Y, I) + I }\)

Implementation:

• to the ionic model 'im' are associated \(N \)= im%N and \(N_a \)= im%Na with \( 0\le N_a \le N \),
• two vectors \(a\in\R^{N_a}\) and \(b\in\R^{N}\) are computed with

  call im%ab(a, b, Y, I, N, Na)

  for \( Y\in\R^N\) and \(I\in\R\) (the interface of the routine 'im%ab' is ionic_term),
• the vectors \(a\) and \(b\) satisfy:
  • \(~~~F_i(Y,I) = a_iy_i + b_i ~~~~~~~\) for \( 1\le i \le N_a\)
  • \(~~~F_i(Y,I) = b_i, ~~~~~~~~~~~~~~~~~\) for \( N_a < i \le N\).

Nota bene

• This implementation is made to benefit from the stanilised ODE solvers in ode_solver_mod,
• A same ionic model has different forms depending on the definition of 'Na'.
  For instance: IONIC_BR and IONIC_BR_0 both represent the Beeler Reuter model but:
  • for IONIC_BR, \( N_a = N_w \) (the number of gating variables) and \( a_i = 1/\tau_i \) for \( 1\le i\le N_w\),
  • for IONIC_BR_0, \( N_a = 0 \) and \( b_i = F_i(Y,I) \) for \( 1\le i\le N\).

Membrane currents

• To the ionic model 'im' are associated \( N_I\)=im%NI membrane ionic currents
  \( ~~~~I_j(Y, I_{\rm app})\) for \(1\le j \le N_I\).
• The vector \( I\in\R^{N_I}\) is computed with

  call ionicModel_IList(I, Y, I_app, type)

  with type the ionic model type (any of IONIC_xxx), see ionicModel_IList.

Author

Charles Pierre

Function/Subroutine Documentation

ionicmodel_clear()

subroutine ionicmodel_mod::ionicmodel_clear ( type(ionicmodel), intent(inout)  im )

private

Destructor.

Definition at line 243 of file ionicModel_mod.f90.

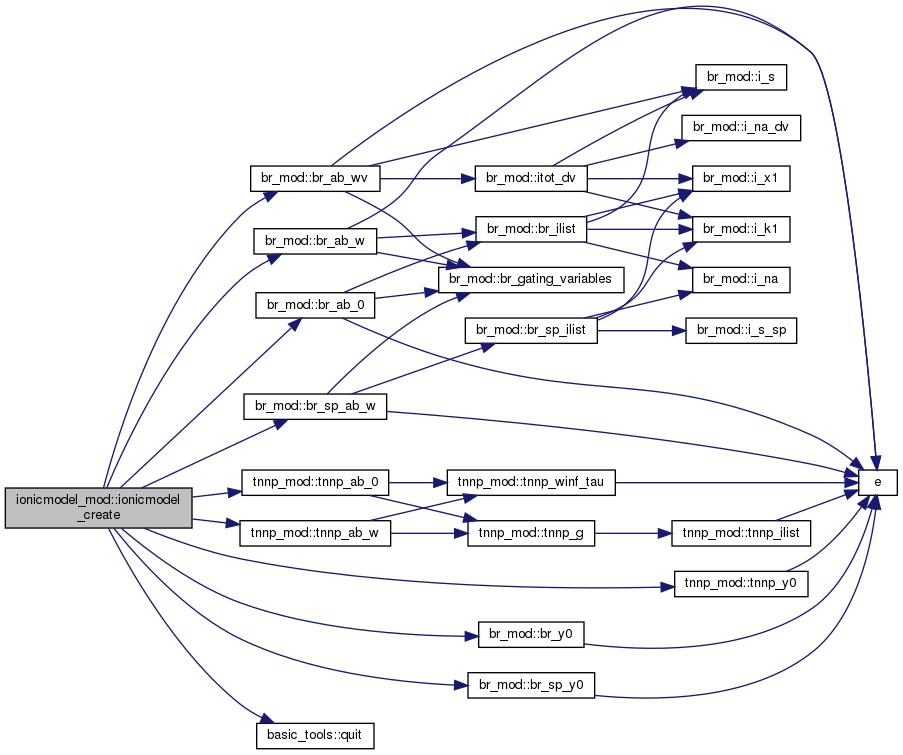
ionicmodel_create()

type(ionicmodel) function ionicmodel_mod::ionicmodel_create ( integer, intent(in)  type )

private

Constructor for the type ionicModel

Parameters

[out]	im	= ionicModel
[in]	type	= ionic model type, any of IONIC_xxx.

Definition at line 265 of file ionicModel_mod.f90.

Here is the call graph for this function:

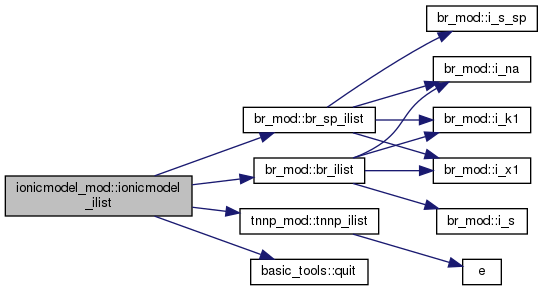
ionicmodel_ilist()

subroutine, public ionicmodel_mod::ionicmodel_ilist	(	real(rp), dimension(:), intent(out)	I,
		real(rp), dimension(:), intent(in)	Y,
		real(rp), intent(in)	I_app,
		integer, intent(in)	type
	)

Membrane ionic currents

Returns an array of all the membrane ionic currents for a given ionci model.

See ionicModel_mod detailed description

Parameters

[out]	I	= membrane ionic currents \( I=(I_1,\dots,I_{N_I} \in \R^{N_I}\)
[in]	Y	= state variable
[in]	I_app	= applied stimulation current
[in]	type	= ionic model type, any of IONIC_xxx.

Definition at line 386 of file ionicModel_mod.f90.

Here is the call graph for this function:

ionicmodel_print()

subroutine ionicmodel_mod::ionicmodel_print ( type(ionicmodel)  im )

private

Print a short description.

Definition at line 357 of file ionicModel_mod.f90.