DERIVED TYPE geoTsf: geometrical transformation of reference cells More...
Data Types | |
| interface | assemble |
| 1- Define the transformation T: K_ref –> K i.e. compute the ytansformation 'T' coefficients More... | |
| interface | clear |
| Destructor. More... | |
| interface | geotsf |
| Geometrical transformation \(T~: K_{\rm ref} \mapsto K \). More... | |
Functions/Subroutines | |
| subroutine | geotsf_clear (g) |
| Destructor for geoTsf type. More... | |
| type(geotsf) function | geotsf_create (dim, nn, y) |
| Constructor for the type geoTsf More... | |
| subroutine | geotsf_assemble (g, type, X, nNd) |
| Define the transformation T: K_ref –> K. More... | |
| subroutine, public | compute_j (g) |
| Compute Jy(i) at the nodes y(:;i) More... | |
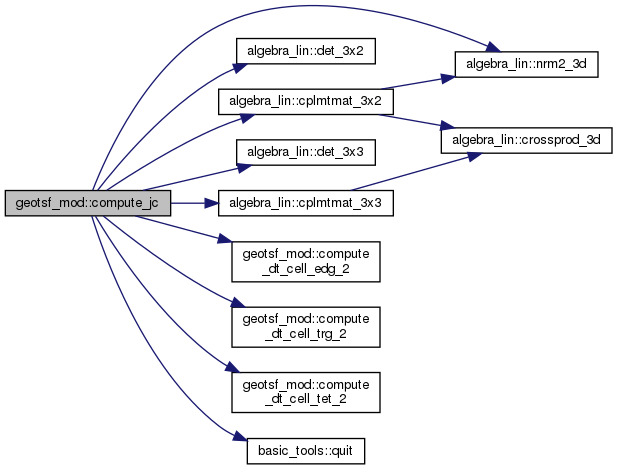
| subroutine, public | compute_jc (g) |
| Computes Jy(i) and Cy(:,:,i) at the nodes y(:;i) More... | |
| subroutine, public | compute_dtjc (g) |
| Compute DTy(:,:,i), Jy(i) and Cy(:,:,i) at the nodes y(:,i) More... | |
| subroutine, public | compute_dtj (g) |
| Compute DTy(:,:,i) and Jy(i) at the nodes y(:,i) More... | |
| logical function, public | belongstocell (x, Y, n, ct) |
| Tests if the node x belongs to the cell with node coordinates Y and of type ct. More... | |
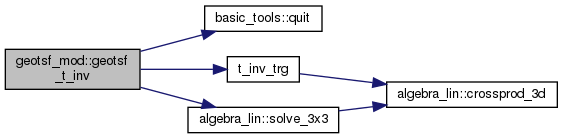
| subroutine, public | geotsf_t_inv (z, X, Y, n, ct) |
| x = 3D node 3D cell of type ct with nodes = A, B, C, ... given by Y(:,1)=A, Y(:,2)=B, ..., Y(:,n) More... | |
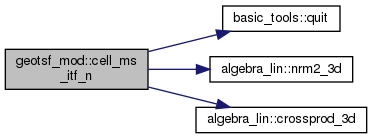
| subroutine, public | cell_ms_itf_n (ms, n, itf_ms, nbItf, g) |
| INPUT :: g = geoTsf, must have been set nbItf = number of interfaces OUTPUT : ms = measure of T(K_ref) n = unit normal to the interfaces of T(K_ref) itf_ms = interface measures. More... | |
| subroutine | compute_dt_cell_edg_2 (g) |
| subroutine | compute_dt_cell_trg_2 (g) |
| subroutine | compute_dt_cell_tet_2 (g) |
Detailed Description
DERIVED TYPE geoTsf: geometrical transformation of reference cells
The derived type geoTsf defines geometrical transformations
\(~~~~~~~~~~ T~: K_{\rm ref} \mapsto K = T(K) ~~~~~~~~~~~~~~~~~~~~~~(1)\)
\(~~~~~~~~~~~~~~~~~~~~~~~ y \mapsto x = T(y) \)
- \( K \subset \R^3 \) is a cell (see cell_mod)
- \( K_{\rm ref} \subset \R^3 \) is a reference cell (see cell_mod)
- \(y \) is the variable name in \(K_{\rm ref} \)
- \(x = T(y)\) is the variable name in \(K \)
A transformation \( T \) as in (1) is defined by
- the cell \( K \) type,
- the cell \( K \) node coordinates.
THE GOAL
Given a set \( y = \{y_1,\dots , y_n\}\) of \( n \) points in \( K_{\rm ref} \) (basically quadrature nodes),
we want to know at each point \( y_i \):
- their images \( Ty_i\in K\) by \( T\),
- the dIfferential \( DT(y_i)\) of \( T \) ,
- the Jacobian \( J(y_i) = {\rm det } \left( DT(y_i)\right)\) of \( T \),
- the complementary matrix \( C(y_i) \) of \( DT(y_i)\) (see definition below).
THE METHOD
To take into account both
- the transformation \(T \)
- the set of points \( y = \{y_1,\dots , y_n\}\) ,
we define an object 'g' of type geoTsf in two steps:
- g = geotsf(dim, n, y)
- dim: the dimension of \( K_{\rm ref}\),
- n: the number of points in \( y\)
- y: the coordinates of the points in \( y\).
- call assemble(g, type, X, nNd)
- type: the geometrical type of \( K \),
- nNd: the number of nodes of \(K\),
- X: the cell \(K\) node coordinates.
Which two steps compute:
- g%T : an array defining the transformation \( T \),
- g%Ty: the images \( Ty\) of the points in \( y \).
Finally,
- computes g%Jy: the Jacobian \( J(y_i) \)call compute_J(g)
- computes g%Jycall compute_JC(g)
computes g%Cy: the complementary matrices \( C(y_i) \) - computes g%DTy: the differentials \( DT(y_i) \)call compute_DTJ(g)
computes g%Jy - computes g%DTy, g%Jy and g%Cy.call compute_DTJC(g)
Complementary matrix definition:
- let \( u_{\rm ref}:~K_{\rm ref} \mapsto R \)
- let \( u = u_{\rm ref} \circ T^{-1}:~K \mapsto R \)
- then:
\(~~~~~~~~~~ \nabla u(x) = C(y) \nabla u_{\rm ref}(y) / J(y) \)
- with \( x = T(y) \)
- mathematically, \(C(y)\) = transpose( co-factor matrix of \( DT(y) \))
Function/Subroutine Documentation
◆ belongstocell()
| logical function, public geotsf_mod::belongstocell | ( | real(rp), dimension(3), intent(in) | x, |
| real(rp), dimension(3,n), intent(inout) | Y, | ||
| integer, intent(in) | n, | ||
| integer, intent(in) | ct | ||
| ) |
Tests if the node x belongs to the cell with node coordinates Y and of type ct.
WARNING : Y is modified (see geoTsf_T_Inv)
Definition at line 603 of file geoTsf_mod.F90.

◆ cell_ms_itf_n()
| subroutine, public geotsf_mod::cell_ms_itf_n | ( | real(rp), intent(out) | ms, |
| real(rp), dimension(3,nbitf), intent(out) | n, | ||
| real(rp), dimension(nbitf), intent(out) | itf_ms, | ||
| integer, intent(in) | nbItf, | ||
| type(geotsf), intent(in) | g | ||
| ) |
INPUT :: g = geoTsf, must have been set nbItf = number of interfaces OUTPUT : ms = measure of T(K_ref) n = unit normal to the interfaces of T(K_ref) itf_ms = interface measures.
Definition at line 749 of file geoTsf_mod.F90.
◆ compute_dt_cell_edg_2()
|
private |
Definition at line 806 of file geoTsf_mod.F90.
◆ compute_dt_cell_tet_2()
|
private |
Definition at line 833 of file geoTsf_mod.F90.
◆ compute_dt_cell_trg_2()
|
private |
Definition at line 818 of file geoTsf_mod.F90.
◆ compute_dtj()
| subroutine, public geotsf_mod::compute_dtj | ( | type(geotsf), intent(inout) | g | ) |
Compute DTy(:,:,i) and Jy(i) at the nodes y(:,i)
Definition at line 539 of file geoTsf_mod.F90.
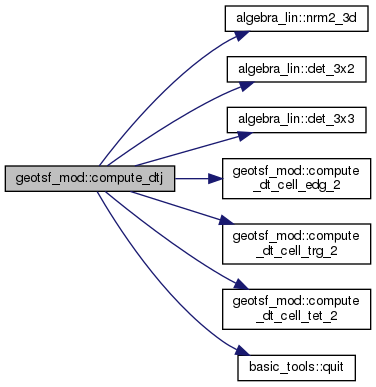
◆ compute_dtjc()
| subroutine, public geotsf_mod::compute_dtjc | ( | type(geotsf), intent(inout) | g | ) |
Compute DTy(:,:,i), Jy(i) and Cy(:,:,i) at the nodes y(:,i)
Definition at line 490 of file geoTsf_mod.F90.
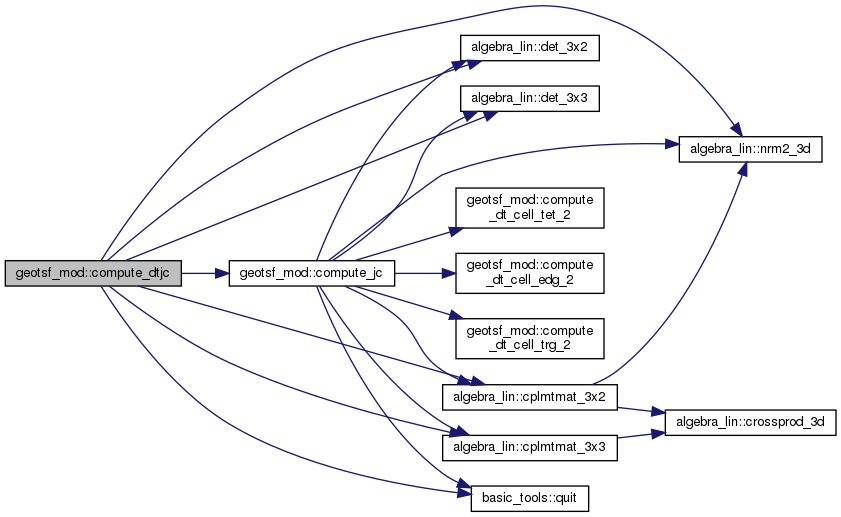
◆ compute_j()
| subroutine, public geotsf_mod::compute_j | ( | type(geotsf), intent(inout) | g | ) |
Compute Jy(i) at the nodes y(:;i)
Definition at line 383 of file geoTsf_mod.F90.
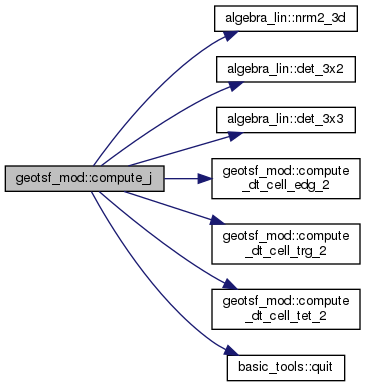
◆ compute_jc()
| subroutine, public geotsf_mod::compute_jc | ( | type(geotsf), intent(inout) | g | ) |
Computes Jy(i) and Cy(:,:,i) at the nodes y(:;i)
Definition at line 428 of file geoTsf_mod.F90.
◆ geotsf_assemble()
|
private |
Define the transformation T: K_ref –> K.
1- Define the transformation T: K_ref –> K i.e. compute the ttansformation 'T' coefficients depending on the type of the cell K and on its node coordinates 'X'
- computate the coordinates of the points 'Ty' in K
Definition at line 250 of file geoTsf_mod.F90.

◆ geotsf_clear()
|
private |
Destructor for geoTsf type.
Definition at line 188 of file geoTsf_mod.F90.
◆ geotsf_create()
|
private |
Constructor for the type geoTsf
- Allocate memory for g%y, g%Ty, g%Jy and g%Cy
- set g%y: the coordinates for the points \(y\) in \( K_{\rm ref}\)
- OUTPUT:
- g : geometrical transformation
- INPUT:
- dim : the dimension of \( K_{\rm ref}\),
- nn : the number of points in \( y\)
- y : the coordinates of the points in \( y\).
Definition at line 216 of file geoTsf_mod.F90.

◆ geotsf_t_inv()
| subroutine, public geotsf_mod::geotsf_t_inv | ( | real(rp), dimension(3), intent(out) | z, |
| real(rp), dimension(3), intent(in) | X, | ||
| real(rp), dimension(3,n), intent(inout) | Y, | ||
| integer, intent(in) | n, | ||
| integer, intent(in) | ct | ||
| ) |
x = 3D node 3D cell of type ct with nodes = A, B, C, ... given by Y(:,1)=A, Y(:,2)=B, ..., Y(:,n)
Output : z R3
EDG : AX = z(1)AB + n, n orthogonal to AB TRG : AX = z(1)AB + z(2)AC + n, n orthogonal to ABC TET : AX = AX = z(1)AB + z(2)AC + z(2)AD
Output : Y is modified : Y(:,1) = AX Y(:,2) = AB Y(:,3) = AC ...
Definition at line 683 of file geoTsf_mod.F90.
 1.8.13
1.8.13