ONE-STEP SOLVERS FOR NON LINEAR ODEs More...
Functions/Subroutines | |
| logical function, public | check_ode_method_nl_1s (method) |
| is 'method' a one-step non-linear ODE solver ? More... | |
| subroutine, public | memsize_ode_nl_1s (n_Y, n_FY, method) |
| required sizes to allocate memory More... | |
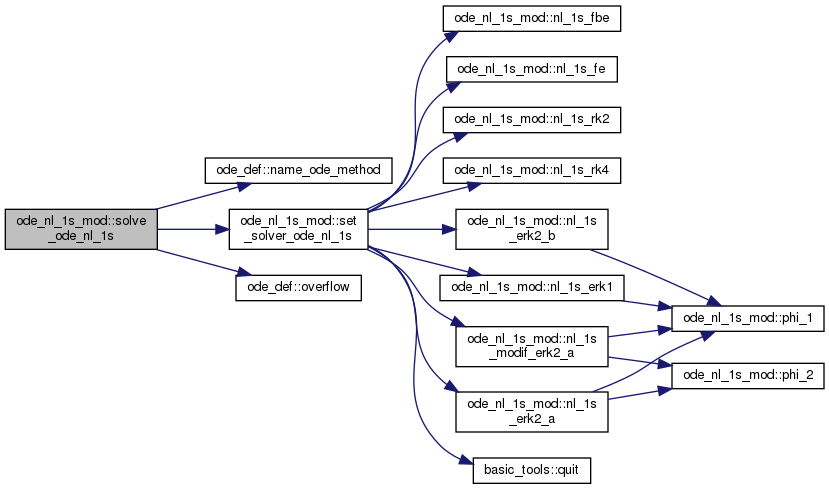
| subroutine, public | set_solver_ode_nl_1s (slv, method) |
| set the solver 'slv' to a predefined solver being given a method More... | |
| subroutine, public | create_ode_nl_1s_sol (sol, pb, method) |
| create memory for the ode_solution structure 'sol' More... | |
| subroutine, public | solve_ode_nl_1s (sol, pb, t0, T, dt, method, out, check_overflow) |
| solve with constant time-step More... | |
| subroutine | nl_1s_fbe (sol, dt, t, pb) |
| FORWARD/BacWard Euler. More... | |
| subroutine | nl_1s_rk2 (sol, dt, t, pb) |
| RK2. More... | |
| elemental subroutine | phi_1 (z) |
| phi_1 = ( exp(z) - 1 ) / z More... | |
| elemental subroutine | phi_2 (z) |
| phi_2 = (exp(z) - z - 1._RP)/z^2 More... | |
| subroutine | nl_1s_fe (sol, dt, t, pb) |
| Forward Euler. More... | |
| subroutine | nl_1s_erk1 (sol, dt, t, pb) |
| Exponential Euler. More... | |
| subroutine | nl_1s_erk2_a (sol, dt, t, pb) |
| Exponential RK2, type A ref = "Explicit Exponential Runge-Kutta Methods for Semilinear
Parabolic Problems" Hochbruck, Ostermann, SIAM J. Numer. Anal. 2005 page 1082, tableau 1, c2 = 1/2. More... | |
| subroutine | nl_1s_erk2_b (sol, dt, t, pb) |
| Exponential RK2, type B ref = "Explicit Exponential Runge-Kutta Methods for Semilinear
Parabolic Problems" Hochbruck, Ostermann, SIAM J. Numer. Anal. 2005 page 1082, tableau 2, c2 = 1/2. More... | |
| subroutine | nl_1s_modif_erk2_b (sol, dt, t, pb) |
| Modified ERK2_B. More... | |
| subroutine | nl_1s_modif_erk2_a (sol, dt, t, pb) |
| Modified ERK2_A. More... | |
| subroutine | nl_1s_rk4 (sol, dt, t, pb) |
| RK4. More... | |
Detailed Description
ONE-STEP SOLVERS FOR NON LINEAR ODEs
One step solvers for ODE_PB_NL, see ode_problem_mod detailed description.
Function/Subroutine Documentation
◆ check_ode_method_nl_1s()
| logical function, public ode_nl_1s_mod::check_ode_method_nl_1s | ( | integer, intent(in) | method | ) |
is 'method' a one-step non-linear ODE solver ?
Definition at line 36 of file ode_NL_1s_mod.f90.
◆ create_ode_nl_1s_sol()
| subroutine, public ode_nl_1s_mod::create_ode_nl_1s_sol | ( | type(ode_solution), intent(inout) | sol, |
| type(ode_problem), intent(in) | pb, | ||
| integer, intent(in) | method | ||
| ) |
create memory for the ode_solution structure 'sol'
Definition at line 114 of file ode_NL_1s_mod.f90.
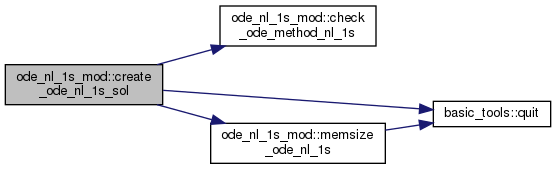
◆ memsize_ode_nl_1s()
| subroutine, public ode_nl_1s_mod::memsize_ode_nl_1s | ( | integer, intent(out) | n_Y, |
| integer, intent(out) | n_FY, | ||
| integer, intent(in) | method | ||
| ) |
required sizes to allocate memory
returns iY, iFY depending on the method
- n_Y = required size for Y
- n_FY = required size for AY, BY
Definition at line 60 of file ode_NL_1s_mod.f90.

◆ nl_1s_erk1()
|
private |
Exponential Euler.
Definition at line 338 of file ode_NL_1s_mod.f90.

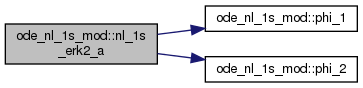
◆ nl_1s_erk2_a()
|
private |
Exponential RK2, type A ref = "Explicit Exponential Runge-Kutta Methods for Semilinear Parabolic Problems" Hochbruck, Ostermann, SIAM J. Numer. Anal. 2005 page 1082, tableau 1, c2 = 1/2.
Definition at line 380 of file ode_NL_1s_mod.f90.
◆ nl_1s_erk2_b()
|
private |
Exponential RK2, type B ref = "Explicit Exponential Runge-Kutta Methods for Semilinear Parabolic Problems" Hochbruck, Ostermann, SIAM J. Numer. Anal. 2005 page 1082, tableau 2, c2 = 1/2.
Definition at line 472 of file ode_NL_1s_mod.f90.

◆ nl_1s_fbe()
|
private |
FORWARD/BacWard Euler.
(y1 - y)/dt = a(y)*y1 + b(y)
updates y := y1
Na=0 => explicit Euler
Definition at line 201 of file ode_NL_1s_mod.f90.
◆ nl_1s_fe()
|
private |
Forward Euler.
Definition at line 309 of file ode_NL_1s_mod.f90.
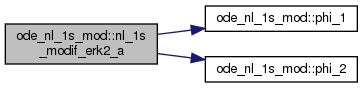
◆ nl_1s_modif_erk2_a()
|
private |
Modified ERK2_A.
Definition at line 607 of file ode_NL_1s_mod.f90.
◆ nl_1s_modif_erk2_b()
|
private |
Modified ERK2_B.
Definition at line 552 of file ode_NL_1s_mod.f90.

◆ nl_1s_rk2()
|
private |
RK2.
Definition at line 233 of file ode_NL_1s_mod.f90.
◆ nl_1s_rk4()
|
private |
RK4.
Definition at line 675 of file ode_NL_1s_mod.f90.
◆ phi_1()
|
private |
phi_1 = ( exp(z) - 1 ) / z
Definition at line 275 of file ode_NL_1s_mod.f90.
◆ phi_2()
|
private |
phi_2 = (exp(z) - z - 1._RP)/z^2
Definition at line 289 of file ode_NL_1s_mod.f90.
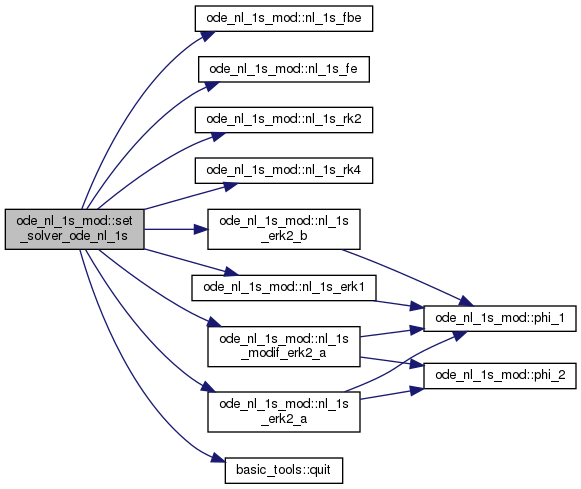
◆ set_solver_ode_nl_1s()
| subroutine, public ode_nl_1s_mod::set_solver_ode_nl_1s | ( | procedure(ode_nl_1s_solver), pointer | slv, |
| integer, intent(in) | method | ||
| ) |
set the solver 'slv' to a predefined solver being given a method
Definition at line 82 of file ode_NL_1s_mod.f90.
◆ solve_ode_nl_1s()
| subroutine, public ode_nl_1s_mod::solve_ode_nl_1s | ( | type(ode_solution), intent(inout) | sol, |
| type(ode_problem), intent(in) | pb, | ||
| real(rp), intent(in) | t0, | ||
| real(rp), intent(in) | T, | ||
| real(rp), intent(in) | dt, | ||
| integer, intent(in) | method, | ||
| procedure(ode_output_proc) | out, | ||
| logical, intent(in) | check_overflow | ||
| ) |
solve with constant time-step
Definition at line 136 of file ode_NL_1s_mod.f90.
 1.8.13
1.8.13