DERIVED TYPE graph: sparse matrices of boolean in CSR format
More...
Data Types | |
| interface | clear |
| interface | copy |
| interface | equal |
| check graph equality More... | |
| interface | getrow |
| extract a graph row More... | |
| interface | graph |
| The type graph stores sparse matrices of boolean in CSR format. More... | |
| interface | |
| print a short description More... | |
| interface | setrow |
| set a graph row More... | |
| interface | sortrows |
| sort graph rows in ascending order More... | |
| interface | transpose |
| transpose graph More... | |
| interface | valid |
Functions/Subroutines | |
| subroutine | graph_clear (g) |
| Destructor for the type graph. More... | |
| type(graph) function | graph_create (nnz, nl, nc) |
| Constructor for the type graph More... | |
| integer function | graph_valid (g) |
| Check if the graph structure 'g' is valid. More... | |
| subroutine | graph_print (g) |
| Print a short description of the graph 'g'. More... | |
| subroutine | graph_copy (g, g0) |
| g := g0 More... | |
| logical function | graph_equal (g2, g1) |
| test equality Two graph are equal if the underlying boolean matrices are equal independently of the column storing order More... | |
| subroutine | graph_getrow_1 (sz, p, n, g, ii) |
| Extract row ii of the graph g. More... | |
| subroutine | graph_getrow_2 (p, n, g, ii) |
| Extract row ii of the graph g. More... | |
| subroutine | graph_setrow (g, col, p, ii) |
| subroutine | graph_transpose (g2, g1) |
| Transpose graph. More... | |
| subroutine, public | union (sz, tab, bf1, n, bf2, p, g, rows, m) |
| graph row union More... | |
| subroutine, public | graph_extract (g2, g1, line) |
| line i of g2 = line i of g1 if line(i) = .TRUE. = void otherwise More... | |
| subroutine | graph_sortrows (g) |
| Sort all rows of the graph g. More... | |
| subroutine, public | graph_prod (g, A, B) |
| Matrix product g = A*B. More... | |
| subroutine, public | prod_tab (g, A, B) |
| graph product More... | |
Detailed Description
DERIVED TYPE graph: sparse matrices of boolean in CSR format
The type graph encodes graphs (or more generally hyper-graphs) given by their adjacency matrix.
An hyper-graph is a relation rule \( R\) between the elements of two sets \(E\) and \(F\):
for exemple \( sRe\) if \( s\in e\) between the vertexes \(s\in E\) and the edges \( e \in F\) of a mesh \( \mathcal{T}\).
The adjacency matrix of an hypergraph \( R\) is a matrix of boolean \( M = [m_{ij}]_{i\in E,~ j\in F} \) where:
- \( m_{ij} = \) TRUE if \( i R j \)
- \( m_{ij} = \) FALSE otherwise
The type graph stores the matrix \( M \) in CSR format (Compressed Sparse Rows).
Function/Subroutine Documentation
◆ graph_clear()
|
private |
Destructor for the type graph.
Definition at line 164 of file graph_mod.F90.
◆ graph_copy()
|
private |
g := g0
Definition at line 307 of file graph_mod.F90.
◆ graph_create()
|
private |
Constructor for the type graph
- Parameters
-
[out] g graph [in] nnz(i) = number of non zero entries on line i [in] nl = nulber of lines [in] nc = nulber of columns if nc is unknown when creating the graph, set nc to 0 and reset it afterwards0
Definition at line 188 of file graph_mod.F90.

◆ graph_equal()
|
private |
test equality Two graph are equal if the underlying boolean matrices are equal independently of the column storing order
Definition at line 331 of file graph_mod.F90.

◆ graph_extract()
| subroutine, public graph_mod::graph_extract | ( | type(graph), intent(inout) | g2, |
| type(graph), intent(in) | g1, | ||
| logical, dimension(:), intent(in) | line | ||
| ) |
line i of g2 = line i of g1 if line(i) = .TRUE. = void otherwise
Definition at line 598 of file graph_mod.F90.

◆ graph_getrow_1()
|
private |
Extract row ii of the graph g.
OUTPUT : sz = row ii size p(1:sz) = row ii
INPUT : n = dimension of p WARINIG : n must be larger than sz g = GRAPH ii= row index
Definition at line 380 of file graph_mod.F90.

◆ graph_getrow_2()
|
private |
Extract row ii of the graph g.
OUTPUT : p(1:n) = row ii
INPUT : n = dimension of p WARINIG : It is implicitely assumed that p has the expected size g = graph ii= row index
Definition at line 421 of file graph_mod.F90.

◆ graph_print()
|
private |
Print a short description of the graph 'g'.
Definition at line 291 of file graph_mod.F90.
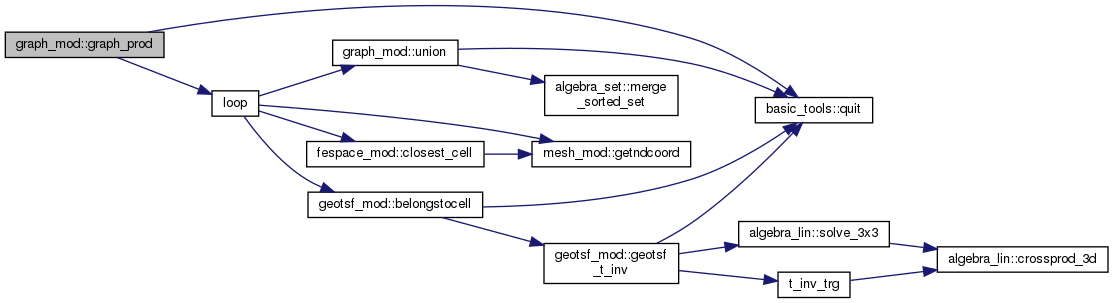
◆ graph_prod()
| subroutine, public graph_mod::graph_prod | ( | type(graph), intent(inout) | g, |
| type(graph), intent(in) | A, | ||
| type(graph), intent(in) | B | ||
| ) |
Matrix product g = A*B.
Definition at line 679 of file graph_mod.F90.
◆ graph_setrow()
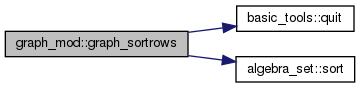
◆ graph_sortrows()
|
private |
Sort all rows of the graph g.
Definition at line 648 of file graph_mod.F90.
◆ graph_transpose()
|
private |
Transpose graph.
NOTE = The rows of the transpose graph are sorted increasingly
Definition at line 485 of file graph_mod.F90.

◆ graph_valid()
|
private |
Check if the graph structure 'g' is valid.
- Parameters
-
[in] g graph to be checked [out] info graph state (>0 means valid)
Definition at line 243 of file graph_mod.F90.
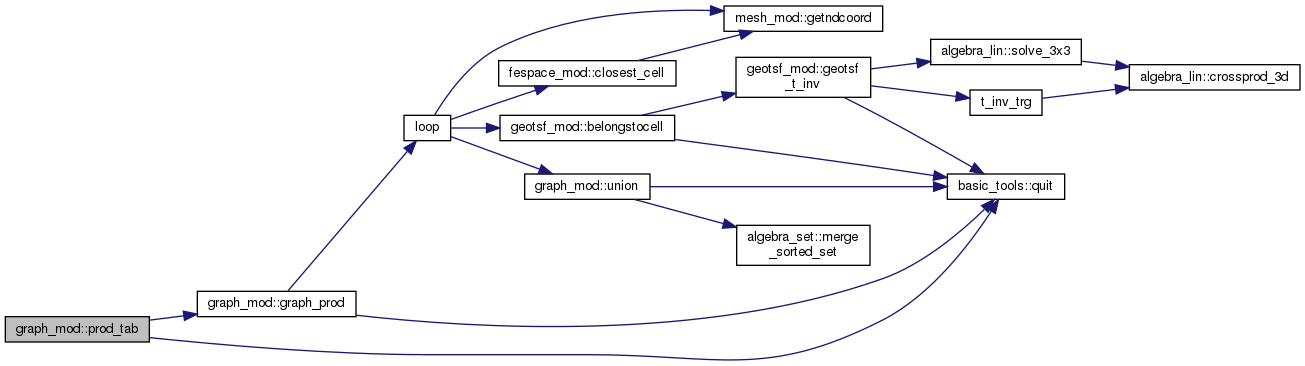
◆ prod_tab()
| subroutine, public graph_mod::prod_tab | ( | type(graph), intent(inout) | g, |
| type(graph), intent(in) | A, | ||
| type(graph), intent(in) | B | ||
| ) |
graph product
g = tA B, tA = transpose(A)
Definition at line 774 of file graph_mod.F90.
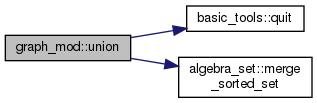
◆ union()
| subroutine, public graph_mod::union | ( | integer, intent(out) | sz, |
| integer, dimension(n), intent(out) | tab, | ||
| integer, dimension(n), intent(out) | bf1, | ||
| integer, intent(in) | n, | ||
| integer, dimension(p), intent(out) | bf2, | ||
| integer, intent(in) | p, | ||
| type(graph), intent(in) | g, | ||
| integer, dimension(m), intent(in) | rows, | ||
| integer, intent(in) | m | ||
| ) |
graph row union
There are sz integers j so that g[i, j] = 1 for at least one i rows
Output : sz = number of such integers tab(1:sz) = these integers tab is of size n and it is assumed that n >= sz
bf1 = buffer array of size n bf2 = buffer array of size p >= gwidth
INPUT : g = graph that must be sorted rows = rows of g to merge n = size of tab, bf1 n = size of rows p = size of bf2
Definition at line 558 of file graph_mod.F90.

 1.8.13
1.8.13