DEFINITION OF FINITE ELEMENT METHODS More...

Functions/Subroutines
subroutine, public	scal_fe (val, nbDof, x, dim, ft)
	Evaluate FE basis functions at point x. More...

subroutine, public	scalgrad_fe (val, nbDof, x, dim, ft)
	Evaluate the gradient of the FE basis functions at point x. More...

subroutine, public	vect_fe (val, nbDof, x, dim, ft)
	Evaluate vector FE basis functions at point x. More...

subroutine, public	vectdiv_fe (val, nbDof, x, dim, ft)
	Evaluate the divergence of the vector FE basis functions at point x. More...

subroutine, public	fe_init (b)
	initialise FE_XXX arrays More...

subroutine	def_fe ()
	Number of DOF for each FE method. More...

subroutine	def_fe_dof_type ()
	DOF types. More...

subroutine	def_fe_dof_geo ()
	DOF geometrical types. More...

subroutine	def_fe_dof_geoelmt ()
	in the cell K : More...

subroutine	def_fe_dof_vtx ()
	FE_DOF_VTX(1:n, i, f) = vertexes of the ref. cell associated to the dof i of the FE method f. More...

subroutine	def_fe_dof_bary ()
	FE_DOF_BARY(1:n, i, f) = barycentric coordinates of the dof i of the FE method f. More...

subroutine	def_fe_func ()
	Finite element function. More...

subroutine	def_fe_dof_nbvtx ()
	FE DOF number of vertexes. More...

subroutine	def_fe_dim ()
	set FE dimension More...

subroutine	def_fe_dof_coord ()
	set FE dof coordinates More...

Variables
type(fe_functions), dimension(fe_tot_nb), public	fe_func
	FE_ARRAY Arrays describing finite element methods. More...

character(len=16), dimension(0:fe_tot_nb), public	fe_name
	Name for each fe method. More...

integer, dimension(fe_tot_nb), public	fe_nbdof
	Number of DOF for each fe method. More...

integer, dimension(fe_tot_nb), public	fe_geo
	Reference cell geometry for each fe method. More...

integer, dimension(fe_tot_nb), public	fe_dim
	Reference cell dimension for each fe method. More...

integer, dimension(fe_max_nbdof, fe_tot_nb), public	fe_dof_geo = -1
	FE_DOF_GEO(i, j) = Geometric type of DOF i of the FE method j. More...

integer, dimension(fe_max_nbdof, fe_tot_nb), public	fe_dof_type = -1
	FE_DOF_TYPE(i,j) = dof type of the DOF i of the FE method j (Lagrange, ...) More...

integer, dimension(fe_max_nbdof, fe_tot_nb), public	fe_dof_geoelmt = -1
	For the FE method j : the associated reference cell is \( K_{ref} \) := FE_GEO(i) More...

integer, dimension(fe_max_nbdof, fe_tot_nb), public	fe_dof_nbvtx = -1
	FE_DOF_NBVTX(i,j) = number of vertexes of the geometric element associated with the DOF i of the FE method j. More...

integer, dimension(cell_max_nbvtx, fe_max_nbdof, fe_tot_nb), public	fe_dof_vtx =-1
	FE_DOF_VTX(1:n,i,j) = for the DOF i of the FE method j : More...

real(rp), dimension(cell_max_nbvtx, fe_max_nbdof, fe_tot_nb), public	fe_dof_bary =0._RP
	FE_DOF_BARY(1:n,i,j) = for the DOF i of the FE method j : More...

type(r_2d), dimension(fe_tot_nb), public	fe_dof_coord
	DOF node coordinates. More...

Detailed Description

DEFINITION OF FINITE ELEMENT METHODS

Choral constants for finite eleemnt methods: FE_xxx, see the list.

DESCRIPTION: finite eleemnt methods are described by

a series of arrays (see the list). They are initiated with
call fe_init()
basis functions, they are in defined fe_func_mod.

Author: Charles Pierre

Function/Subroutine Documentation

◆ def_fe()

subroutine fe_mod::def_fe ( )

private

Number of DOF for each FE method.

Definition at line 276 of file fe_mod.F90.

Here is the call graph for this function:

◆ def_fe_dim()

subroutine fe_mod::def_fe_dim ( )

private

set FE dimension

Definition at line 979 of file fe_mod.F90.

◆ def_fe_dof_bary()

subroutine fe_mod::def_fe_dof_bary ( )

private

FE_DOF_BARY(1:n, i, f) = barycentric coordinates of the dof i of the FE method f.

on the ref cell : dof i coordinates = sum_{j<=n} bary(j) * vertex_j

with vertex_j = FE_DOF_VTX(j, i, f)

with n = FE_DIF_NBVTX(i,f)

Definition at line 776 of file fe_mod.F90.

◆ def_fe_dof_coord()

subroutine fe_mod::def_fe_dof_coord ( )

private

set FE dof coordinates

Definition at line 994 of file fe_mod.F90.

◆ def_fe_dof_geo()

subroutine fe_mod::def_fe_dof_geo ( )

private

DOF geometrical types.

Definition at line 445 of file fe_mod.F90.

◆ def_fe_dof_geoelmt()

subroutine fe_mod::def_fe_dof_geoelmt ( )

private

in the cell K :

FE_DOF_GEOELMT(i,f) = index of the geometrical element associated with the dof i of the FE method f

with : K = ref cell associated with the FE method f

Definition at line 549 of file fe_mod.F90.

◆ def_fe_dof_nbvtx()

subroutine fe_mod::def_fe_dof_nbvtx ( )

private

FE DOF number of vertexes.

Definition at line 960 of file fe_mod.F90.

◆ def_fe_dof_type()

subroutine fe_mod::def_fe_dof_type ( )

private

DOF types.

Definition at line 350 of file fe_mod.F90.

◆ def_fe_dof_vtx()

subroutine fe_mod::def_fe_dof_vtx ( )

private

FE_DOF_VTX(1:n, i, f) = vertexes of the ref. cell associated to the dof i of the FE method f.

with n = FE_DIF_NBVTX(i,f)

Definition at line 642 of file fe_mod.F90.

◆ def_fe_func()

subroutine fe_mod::def_fe_func ( )

private

Finite element function.

Definition at line 905 of file fe_mod.F90.

Here is the call graph for this function:

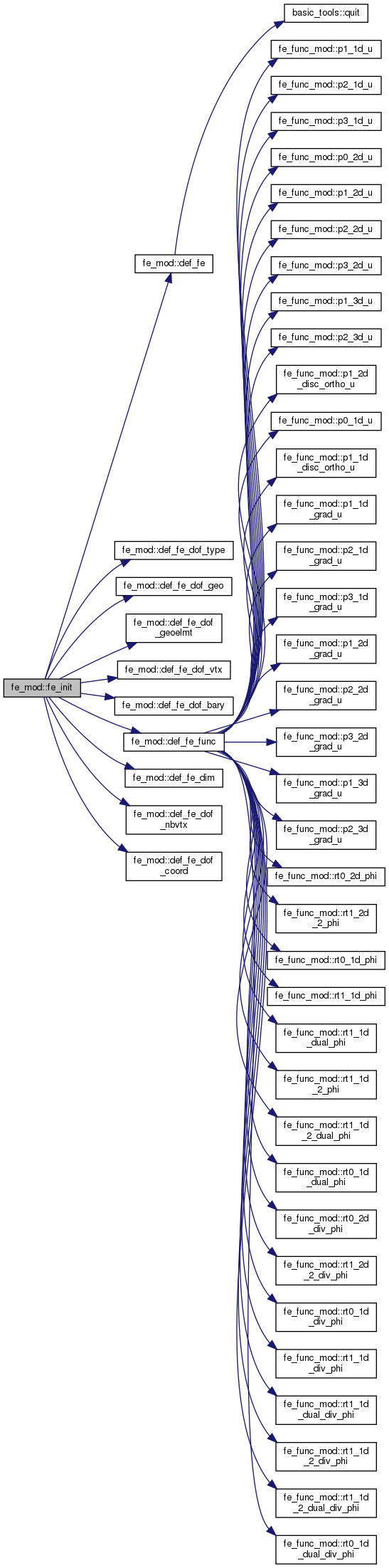
◆ fe_init()

subroutine, public fe_mod::fe_init ( logical, intent(in) b )

initialise FE_XXX arrays

Definition at line 252 of file fe_mod.F90.

Here is the call graph for this function:

◆ scal_fe()

subroutine, public fe_mod::scal_fe	(	real(rp), dimension(nbdof), intent(out)	val,
		integer, intent(in)	nbDof,
		real(rp), dimension(dim), intent(in)	x,
		integer, intent(in)	dim,
		integer, intent(in)	ft
	)

Evaluate FE basis functions at point x.

val(ii) = u_i(x) for the fe method ft

Definition at line 136 of file fe_mod.F90.

Here is the call graph for this function:

◆ scalgrad_fe()

subroutine, public fe_mod::scalgrad_fe	(	real(rp), dimension(dim, nbdof), intent(out)	val,
		integer, intent(in)	nbDof,
		real(rp), dimension(dim), intent(in)	x,
		integer, intent(in)	dim,
		integer, intent(in)	ft
	)

Evaluate the gradient of the FE basis functions at point x.

val(:,ii) = grad u_i(x) for the fe method ft

Definition at line 166 of file fe_mod.F90.

Here is the call graph for this function:

◆ vect_fe()

subroutine, public fe_mod::vect_fe	(	real(rp), dimension(dim,nbdof), intent(out)	val,
		integer, intent(in)	nbDof,
		real(rp), dimension(dim), intent(in)	x,
		integer, intent(in)	dim,
		integer, intent(in)	ft
	)

Evaluate vector FE basis functions at point x.

val(:,ii) = phi_i(x) for the fe method ft

Definition at line 195 of file fe_mod.F90.

Here is the call graph for this function:

◆ vectdiv_fe()

subroutine, public fe_mod::vectdiv_fe	(	real(rp), dimension(nbdof), intent(out)	val,
		integer, intent(in)	nbDof,
		real(rp), dimension(dim), intent(in)	x,
		integer, intent(in)	dim,
		integer, intent(in)	ft
	)

Evaluate the divergence of the vector FE basis functions at point x.

val(ii) = div phi_i(x) for the fe method ft

Definition at line 225 of file fe_mod.F90.

Here is the call graph for this function:

Variable Documentation

◆ fe_dim

integer, dimension(fe_tot_nb), public fe_mod::fe_dim

Reference cell dimension for each fe method.

Definition at line 74 of file fe_mod.F90.

◆ fe_dof_bary

real(rp), dimension(cell_max_nbvtx,fe_max_nbdof,fe_tot_nb), public fe_mod::fe_dof_bary =0._RP

FE_DOF_BARY(1:n,i,j) = for the DOF i of the FE method j :

barycentric coordinates of the node associated with that DOF relatively to the associated vertexes = FE_DOF_VTX(1:n,i,j)

with n = FE_DOF_NBVTX(i,j)

Definition at line 121 of file fe_mod.F90.

◆ fe_dof_coord

type(r_2d), dimension(fe_tot_nb), public fe_mod::fe_dof_coord

DOF node coordinates.

Definition at line 125 of file fe_mod.F90.

◆ fe_dof_geo

integer, dimension(fe_max_nbdof,fe_tot_nb), public fe_mod::fe_dof_geo = -1

FE_DOF_GEO(i, j) = Geometric type of DOF i of the FE method j.

Definition at line 78 of file fe_mod.F90.

◆ fe_dof_geoelmt

integer, dimension(fe_max_nbdof,fe_tot_nb), public fe_mod::fe_dof_geoelmt = -1

For the FE method j : the associated reference cell is \( K_{ref} \) := FE_GEO(i)

if FE_DOF_GEO(i,j) = CELL_VTX then FE_DOF_GEOELMT(i,j) = associated vertex index in the cell \( K_{ref} \)

if FE_DOF_GEO(i,j) = CELL_ED then FE_DOF_GEOELMT(i,j) = associated edge index in the cell \( K_{ref} \)

else FE_DOF_GEOELMT(i,j) = associated face index in the cell \( K_{ref} \)

Definition at line 99 of file fe_mod.F90.

◆ fe_dof_nbvtx

integer, dimension(fe_max_nbdof,fe_tot_nb), public fe_mod::fe_dof_nbvtx = -1

FE_DOF_NBVTX(i,j) = number of vertexes of the geometric element associated with the DOF i of the FE method j.

Definition at line 104 of file fe_mod.F90.

◆ fe_dof_type

integer, dimension(fe_max_nbdof,fe_tot_nb), public fe_mod::fe_dof_type = -1

FE_DOF_TYPE(i,j) = dof type of the DOF i of the FE method j (Lagrange, ...)

Definition at line 82 of file fe_mod.F90.

◆ fe_dof_vtx

integer, dimension(cell_max_nbvtx,fe_max_nbdof,fe_tot_nb), public fe_mod::fe_dof_vtx =-1

FE_DOF_VTX(1:n,i,j) = for the DOF i of the FE method j :

vertexes of the geometric element associated with that DOF in \( K_{ref} \)

with n = FE_DOF_NBVTX(i,j)

Definition at line 112 of file fe_mod.F90.

◆ fe_func

type(fe_functions), dimension(fe_tot_nb), public fe_mod::fe_func

FE_ARRAY Arrays describing finite element methods.

Finite element functions tab

Definition at line 62 of file fe_mod.F90.

◆ fe_geo

integer, dimension(fe_tot_nb), public fe_mod::fe_geo

Reference cell geometry for each fe method.

Definition at line 71 of file fe_mod.F90.

◆ fe_name

character(len=16), dimension(0:fe_tot_nb), public fe_mod::fe_name

Name for each fe method.

Definition at line 65 of file fe_mod.F90.

◆ fe_nbdof

integer, dimension(fe_tot_nb), public fe_mod::fe_nbdof

Number of DOF for each fe method.

Definition at line 68 of file fe_mod.F90.

Functions/Subroutines

Variables

Detailed Description

Function/Subroutine Documentation

◆ def_fe()

◆ def_fe_dim()

◆ def_fe_dof_bary()

◆ def_fe_dof_coord()

◆ def_fe_dof_geo()

◆ def_fe_dof_geoelmt()

◆ def_fe_dof_nbvtx()

◆ def_fe_dof_type()

◆ def_fe_dof_vtx()

◆ def_fe_func()

◆ fe_init()

◆ scal_fe()

◆ scalgrad_fe()

◆ vect_fe()

◆ vectdiv_fe()

Variable Documentation

◆ fe_dim

◆ fe_dof_bary

◆ fe_dof_coord

◆ fe_dof_geo

◆ fe_dof_geoelmt

◆ fe_dof_nbvtx

◆ fe_dof_type

◆ fe_dof_vtx

◆ fe_func

◆ fe_geo

◆ fe_name

◆ fe_nbdof