Functions/Subroutines
program	eigen_laplacian_2d
	Solves the Laplacian eigenvalue problem More...

subroutine	pmv_m (y, x)
	Matrix-vector product x –> M*x. More...

subroutine	kinv_pcg (y, ierr, x)

subroutine	kinv_mumps (x, ierr, y)

subroutine	residual ()

Function/Subroutine Documentation

◆ eigen_laplacian_2d()

program eigen_laplacian_2d ( )

Solves the Laplacian eigenvalue problem

\(~~~~~ -\Delta u = \lambda u ~~~\) on \(~~~ \Omega= [0,1]^2 \)

with homogeneous Neumann boundary conditions.

Discretisation: finite element method on \( X_h \subset {\rm H}^1(\Omega) \)
we get the symmetric and generalised eigen-problem: \(~~~~ S U = \lambda \, M U \)

\( X_h\) is a \( P^k \) Lagrange finite element space
\( S \) the stiffness matrix relative to the product \( (u,v) \longrightarrow \int_\Omega \nabla u\cdot\nabla v \,\dx\)
\( M \) the mass matrix relative to the product \( (u,v) \longrightarrow \int_\Omega u\,v \,\dx\)

Method:

Arnoldi iterative solver
shift-invert mode, shift factor = \( \sigma \)
\( ~~~~~~~ \frac{1}{\lambda - \sigma} U = K^{-1} M U \) with \( K = S - \sigma M\)
solver for the linear system inversions \(K\,x = y \); Krylov iterative CG

Charles PIERRE, October 2020.

Definition at line 33 of file eigen_Laplacian_2D.f90.

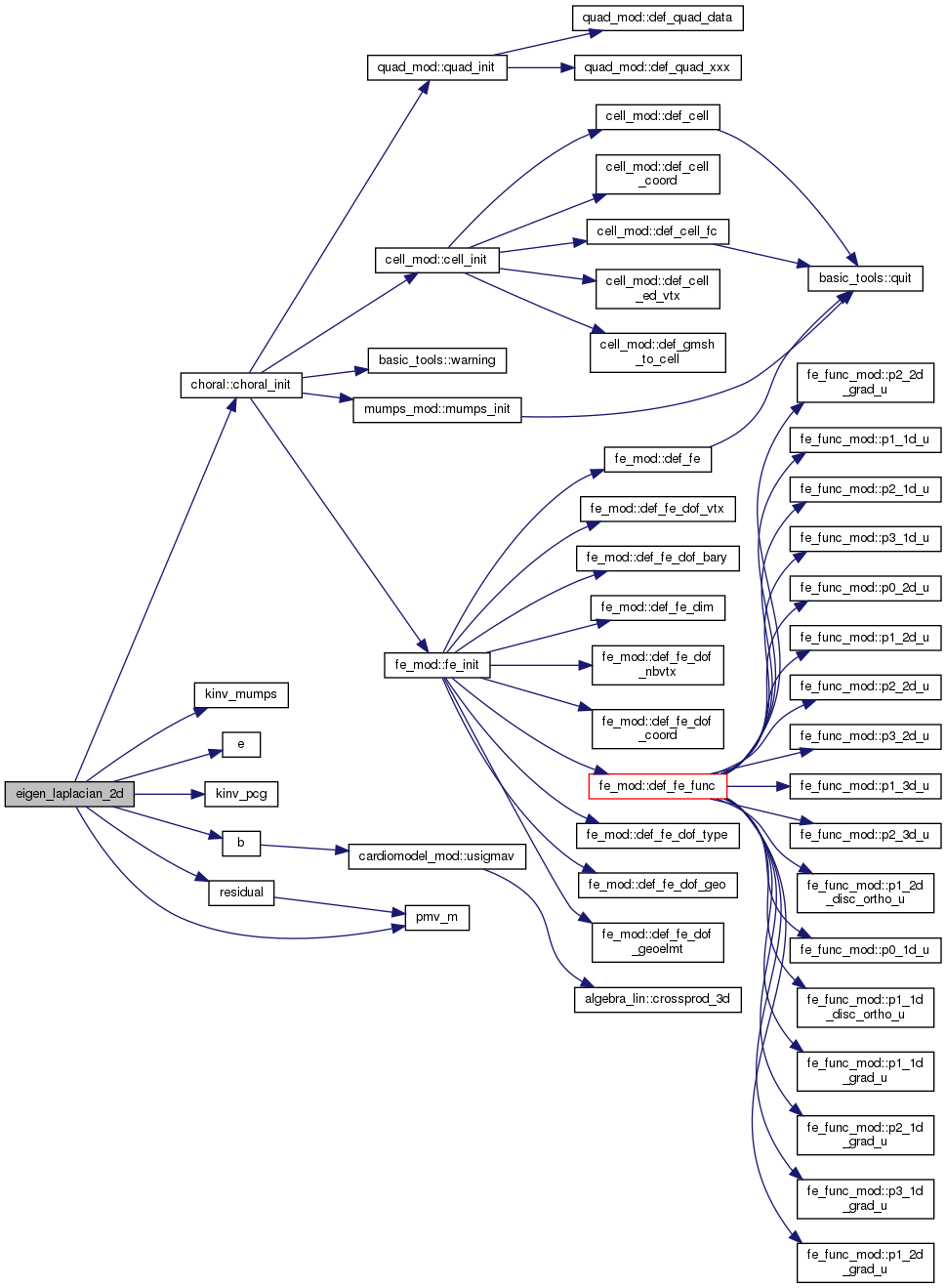
Here is the call graph for this function:

◆ kinv_mumps()

subroutine eigen_laplacian_2d::kinv_mumps	(	real(rp), dimension(:), intent(inout)	x,
		logical, intent(out)	ierr,
		real(rp), dimension(:), intent(in)	y
	)

Definition at line 307 of file eigen_Laplacian_2D.f90.

◆ kinv_pcg()

subroutine eigen_laplacian_2d::kinv_pcg	(	real(rp), dimension(:), intent(inout)	y,
		logical, intent(out)	ierr,
		real(rp), dimension(:), intent(in)	x
	)

Definition at line 293 of file eigen_Laplacian_2D.f90.

◆ pmv_m()

subroutine eigen_laplacian_2d::pmv_m	(	real(rp), dimension(:), intent(out)	y,
		real(rp), dimension(:), intent(in)	x
	)

Matrix-vector product x –> M*x.

Definition at line 283 of file eigen_Laplacian_2D.f90.

◆ residual()

subroutine eigen_laplacian_2d::residual ( )

Definition at line 319 of file eigen_Laplacian_2D.f90.